| « Strange dry shadows | Bad Snow, Part II, and Some History » |
A rare heliac arc? (plus six others)
The day starts sunny and bright, but later you note a slight muting of the surrounding landscape. It is still bright enough, but you feel less heat bearing down. Apparently, a thin veil of high clouds has slowly and silently appeared above.
When this happens, please take a few seconds to look up and see what these clouds are up to. Do they have their crystals lined up for one or more arcs, or are they oriented randomly, giving a halo with perhaps a sun dog or two? To the trained eye, the chances are high that such a veil will give rewards, even when no crystals are present. But the crystals give so much more, particularly when they line up in various ways.
Wandering, somewhat exhausted, on the hillside above Index, WA last Monday, I got this very sense of a muted landscape. So, I found a break in the trees, looked up, and instantly felt recharged. A colorful circumzenithal arc had appeared, which by itself is always a treat. But I was also awed by several other arcs and a very diffuse 22-degree halo. Excitedly, I took photos and scrambled around trees and rock for a more complete view.
(As with all images here, click on the image to see a larger view.)
Due to the complex way the eye and brain discerns light and patterns versus the much simpler way of a camera, the patterns are much more distinct when viewed direct by eye. But the above composition has my attempt to compensate the original photo at left, with some contrast enhancement in the middle version, and markings on the right version.
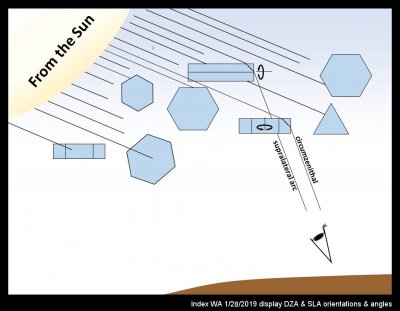
The band of color at the intersection of CZA and SLA is from the oriented prism crystals of the circumzenithal arc (CZA). Their formation is relatively common I think, though a group of observers in Germany apparently finds their occurrence there to be only about 13 times per year (https://www.atoptics.co.uk/halo/whyinfr.htm). What is most remarkable to me is not their colors, but the fact that formation of distinct colors requires that the crystals stay extremely level as they fall (deviations of only a few degrees would wash out the colors). My sketch below shows roughly what is going on here:
(Hold on for a moment, and I'll get to the rare heliac arc below.)
The circumzenithal arc arises when tabular prism-shaped crystals (like small hexagonal frisbees) appear to hover like flying saucers as they fall. My drawing shows the side view, so you cannot see the 6-sided nature from this view. The light enters the top of the crystal, near the edge, refracts (bends down slightly) inside the crystal, and then bends further upon exiting the side of the crystal. The light rays are drawn as black lines (the angles were calculated via Snell's law), reflecting or refracting off a crystal and then hitting the observer's eye as cartooned at the bottom. This refraction separates the colors exactly as a glass prism does*. The blue gets bent more than the red, so the blue color appears higher above the sun. The breadth of the arc arises from the different ways the crystal can spin about the vertical axis as shown in the drawing. The arc itself is the sunward edge of a great circle around the zenith straight above you.
The intersecting SLA arc is called the supralateral. It also arises from highly oriented crystals, but instead of tabular, these crystals are long, pencil-shaped ones laying horizontally. Like the previous CZA case with its tabular crystals, these crystals can also spin about the hexagonal symmetry axis, but in this case, this axis lays horizontal as shown. These crystals also can spin about the vertical axis. Picture them like pencils that can roll and spin on the floor, but can never tumble end-over-end.
If you have trouble seeing how crystals can lay horizontal like this while falling, you are in good company. The first group who explained some of these arcs thought they fell thin-edge to the ground, that is, in a way to maximize their fallspeed J. M. Pertner and F. M. Exner (2nd edition to Meteorologische Optik, 1922) had the fall orientations wrong, but they still had the right explanation in terms of the crystal angles. (Alfred Wegener, of continental-drift-theory fame, was a meteorologist in this same period and knew the correct orientation. Here's to you Alfred!) But, as Robert Greenler writes in his book Rainbows, Halos, and Glories (Cambridge Univ. Press, 1980), just drop some blades of grass in the air and see how they tend to fall--you will see that they oscillate about the horizontal. Ditto for watching leaves fall. To lie nearly perfectly horizontal, the crystals must be relatively small, but not too small. Those too small or too large will tumble, destroying the interesting optical effects.
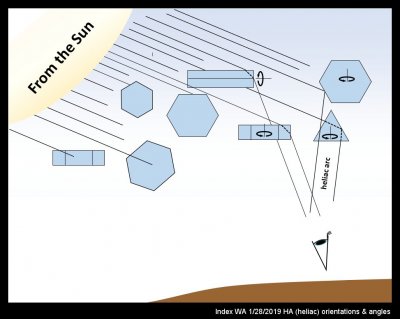
Now about that rare heliac (HA) arc-
After viewing the first photo above, I noticed another faint arc almost directly above, and one I'd never noticed before. In looking through Greenler's book and the above atmospheric optics website (atoptics.co.uk), the only arc that fit the position was the heliac arc (HA). But even in the historically famous atmospheric displays given in those sources, this arc is barely discernable. Indeed, David Lynch and William Livingston in their excellent book Color and Light in Nature (Cambridge Univ. Press, 1995) write "The same crystals responsible for Parry arcs are expected to produce another halo called the heliac arc. It has not been well observed and possibly not at all." Well, this is a rare find indeed.
But despite its rarity, the origin of the heliac arc is one of the simplest: just mirror reflection off a prism face (see sketch above). However, for such a reflection to produce an arc, the crystals must not only lie horizontal, as in those for the supralateral arc (SLA), but also cannot spin on the long axis. So, these crystals are long like those for the SLA, but also have one flat prism face always facing the ground below. In fact, and you can work this out yourself, the same angle comes from an interior reflection as shown in the sketch by the path through the triangle. That is, the light bending at the two surfaces due to refraction exactly cancel. (By the way, such long, triangular columns do exist in the atmosphere. I cannot know from viewing the arc that they were up there, but they have been detected in clouds and also in the laboratory.) Given the Sun's position at the time and place, I calculated the top of the heliac arc to lie just 7 degrees past zenith (straight up). This position seems roughly consistent** with the calculated angles of the other arcs and the photo.
Note that the crystals in the clouds are rarely as perfect as the drawings suggest. Like us, they are usually a little messed up, but the angles between the faces are exactly the 60- and 90 degrees shown.
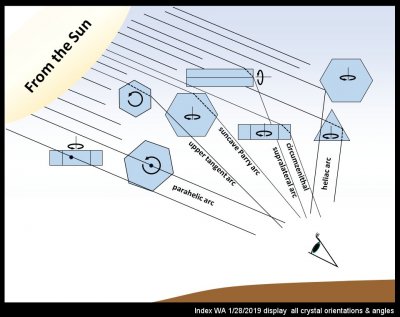
Other arcs nearer the Sun appear in the purple oval of the first picture, but it helps to adjust the contrast for those specifically. The image below shows my attempt to image them.
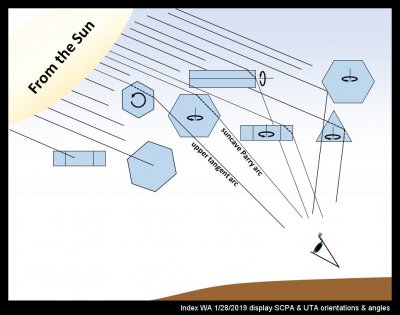
The top one marked SCPA is the suncave Parry arc. This arc is also due to long columnar crystals laying flat like those for the heliac arc. But the rays for this arc pass through two prism faces without a reflection as shown in the sketch. As with the heliac crystals, the long columns can rotate about the vertical, but in no other way. See the sketch below.
Amazingly, two other arcs come from the same ray path: the upper tangent arc (UTA) and the 22-degree halo. As the diagram shows, the crystals for the UTA also rotate about their long axis (and thus rotate about two axes). For the 22-degree halo, the crystals can rotate about all three axes (not shown in the above sketch). These crystals tumble and twist randomly, and as a result, produce an arc that can make a complete circle around the sun. Hence the name 'halo'. I tried to capture it together with two other arcs in the picture below.
The 22-degree halo is very indistinct in this particular image and this display. But you can readily find a clearer example in other displays elsewhere, for other times and other places. Indeed, of all the arcs here, the 22-degree halo is probably the most common. The same survey by the German group (https://www.atoptics.co.uk/halo/whyinfr.htm) finds this halo to be observed on average on 100 days of a given year, at least in Germany. Typically, one sees only parts of the 22-degree halo, such as the sun dogs, which occur where the halo crosses the parahelic arc (PA). The picture above does show a slight brightening where the halo crosses the PA.
The PA, as shown as coming from the bottom crystals in the sketch above, is another arc due to reflections off horizontally laying crystals. It differs from the heliac arc (HA) in that the rays instead reflect off the vertical faces. These faces can either be the prism faces of tabular crystals (the same crystals responsible for the CZA) or the end faces of the columns (same crystals as for the UTA, SCPA, SCA, and HA). Curiously, the parahelic arc (PA), also known as the parahelic circle, is rarely observed: the German survey finding it just 4 days per year on average. Of course, one may find small parts of this circle more often than finding the entire PA. As the sketch shows, this arc passes through the Sun. A little geometry should convince you that it will be observed at a fixed elevation around the zenith. Imagine a white, horizontal hula-hoop above you, and you get the right picture of the full parahelic circle. The first time I recognized it in the sky (almost exactly 20-years ago), it was the full circle, and it appeared huge. It is huge and it is rare. But apparently not as rare as the heliac arc.
I will understand if you say you are underwhelmed by my images here of some of these arcs. You can easily find clearer displays in the literature or web****. But you will be hard-pressed to find a clearer example of the heliac arc. Look for it, when the clouds are right.
--JN
* You can observe this exact prism effect with a straight-sided glass of water on a windowsill if the sun can strike the top of the water at a low enough angle (below about 45 degrees) and the floor area below the window is dark. In this case, the liquid water is forming a 90-degree angle from the top surface to the side, and the glass holding the water has essentially no effect on the resulting spectrum.
** I did not have a scale, but judging from the direction of the trees, the HA appears to be a little past the zenith, away from the sun. And if we circumscribe a circle to the bottom of the CZA, calling the center point the zenith, the radius at 21 degrees (as calculated--see below), then the HA may be at about the right position. The difference between the SCPA and CZA is about the same as that between the CZA and the HA, as the numbers below predict.
**** Including here. Click on the "atmospheric optics" category on the right side (or just below) to see them.
----------------------------------------------
Note 1: The best example of a heliac arc display is the "Neklid display" from 2014:
http://www.haloblog.net/2016/03/06/neklid-antisolar-arcs-case-closed/
Note 2: For the above sketch, I calculated the angles using a) The solar angle of 22.9 degrees off the horizon or 67.1 degrees from the zenith, according to date of 1/28/2019 at 1:00 pm at the lat. and long. of Index, WA. b) An index of refraction of visible light in ice of 1.31, and c) Snell's law.
Angles from the zenith in degrees, and in the Sun-me-zenith plane are
HA: -7.1 (i.e., away from Sun)
CZA & SLA: 21.3
SCPA: 39.8
UTA & 22-degree halo:45.1
Sun & PA: 67.1
All the angles in the sketch, including those of the rays to the crystals, the rays in the crystals, and the rays to the eye, are the computed values and drawn as accurately as possible. The crystals, of course, are not to scale.