Why does snow seem to harden after an avalanche?

Those unfortunate few who have been buried in an avalanche often observe the snow, once stopped, has hardened. Some liken it to concrete. Whereas the powder before the avalanche seemed light and easy to move, once buried, the victim finds it impossible to move.

I have never had that experience, though I find the observation reasonable. For example, on a recent hike up a snow-covered hillside, I used snowshoes to avoid "postholing" through the snow. But when I came to a region where snow had slid down, I removed the snowshoes and easily walked on the surface.

You can see in that picture that considerable debris was present in that case, though it is unimportant for the present discussion.

An article I read last year about a similar event, yet on a vastly larger scale, reported quite the opposite: the ice melting by its tumbling fall down the mountain. Here is the relevant excerpt:

This last article got me wondering because I had come across some claims that the tumbling of the snow creates frictional heat that melts some of the snow, resulting in refreezing into the harder "concrete" snow after the avalanche. Could that actually be true?

Quick answer: Very unlikely.

I'll just address that case here, and consider the case from the article in part 2.

Calculating the amount of heating to the snow is essentially the same basic physics calculation as that for calculating air temperature at various elevations in the atmosphere. Physicists had found long ago that introducing the abstract concept of energy to a problem greatly simplified the calculations. For example, when air at high elevation somehow descends to a lower elevation, one can easily calculate how much its temperature rises using the following energy argument:

1) Air (or ice or meltwater) up high: larger "potential" energy P, smaller "internal" (thermal) energy U.

2) Air upon descending has the same total energy: P+U does not change.

3) Air (or ice or meltwater) down low: small potential energy, but larger thermal energy (i.e., warmer).

The internal energy gained by the descending air warms it up by an amount that depends on its "heat capacity" C. If there are droplets or crystals in the air, then this gain of additional internal energy will partly go into the phase changes of evaporation, sublimation, or melting.

In the case of falling ice, the relevant phase change is melting.

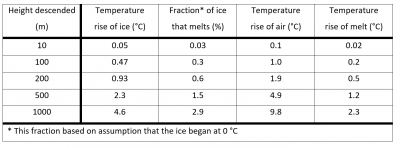
In the left column you see the height descended, from 10 meters (~33') to 1000 meters (over 1/2 mile). Even if the ice tumbled down 1000 meters, it would warm by less than 5 C (9 F), and this amount is less than the amount that the surrounding air has warmed. (That is, despite a little warming, it will nevertheless be colder than the surrounding air.) Most avalanches are probably much closer to 100 m of descent, which is less than 1 degree F. Moreover, once the ice reaches the melting point, it takes considerable more heating to actually melt it. For example, if the ice had begun at the melting point, only 3% of it could melt, even after falling 1000 meters.

So, the conclusion here is that no, the tumbling of snow in an avalanche is very unlikely to cause any significant fraction of the ice to melt. (Of course, that might seem obvious in retrospect, after all, if the snow sometimes partly melts then surely in other cases it must fully melt. Yet have any avalanches ever been observed to transform into a river?)

So, why does the snow harden so much?

Probably this is much like the hardening of snow when you make a snowball. Various physical processes may be involved in that, but the main cause is probably that the packing greatly increases the surface contact, and when two points of ice contact, they sinter. Sintering creates strong bonds. In clays, the sintering process results in pottery, which is extremely hard.

The analysis here can also be applied to rivers. For instance, sometimes you might hear the idea that moving water doesn't freeze because the motion warms it up. You can see from the table that the temperature rise from descending is tiny. What is happening instead is that the motion tends to mix the water, which makes the river temperature uniform. Thus, to freeze, the entire river must cool below 0 C, instead of just the top, as happens, for example, with ponds and puddles. Rivers rarely freeze simply because they began as warm water that continued to mix as it flowed.

--JN