| « Bentley’s Most Singular Observation | Blues and Whites of Snow and Ice » |
Why six?
[This is the sixth in the series of re-posted articles, from 2011.]
Why do so many snow crystals look about the same when rotated by 1/6 of a turn? What’s the origin of the six-fold symmetry? Why not five or seven, as Kepler asked(1)?
Since it always happens, when it begins to snow, that the first particles of snow adopt the shape of small, six-cornered stars, there must be a particular cause; for if it happened by chance, why would they always fall with six corners, and not with five, or seven, as long as they are still scattered and distinct, and before they are driven into a confused mass?
Though we can now answer the last two questions, the first, as pondered by Bentley and many others, still awaits a complete answer.
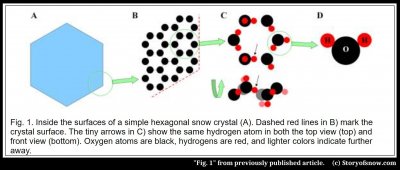
The thing that allows (but does NOT cause) the crystal to have six-fold symmetry comes down to in its internal crystalline lattice of water molecules. Specifically, if you could zoom in about a million times into any region of a snow crystal, such as the corner in figure 1A below, you would see a lattice of hexagonal rings B) – like a microscopic internal honeycomb. The oxygen atoms (black) in each ring have the six-fold symmetry. But if you further examine the rings, notice that all of them are rotated by 30º in relation to the crystal hexagon in A).
However, if you look even closer, such that you can see the orientations of the molecules, and turn the ring on its side, as in C), you will see that in fact the ring is not perfectly six-fold symmetric and it’s not even flat! The honeycomb inside ice is not so simple. But if you sought the overly simplified answer to the origin of the “6”, find it in the hexagonal lattice. Call that the answer for the easily persuaded. There are serious problems though with that answer.
The simple answer specifically has two problems. The internal honeycomb just gives us a similarity between the ice lattice and the crystal form – it suggests that the crystal may develop six-fold symmetry. But just because a crystal may have six sides doesn’t mean it will have six sides. Or, to use one of Kepler’s examples, a beehive also has an internal honeycomb structure, and yet from the outside it appears blobby and nondescript – hardly six-sided.
So, just because the internal structure in snow consists of tiny hexagonal rings doesn’t mean the crystal should look the same when given a turn of 1/6. Moreover, to say that the six-sided nature comes from the hexagonal lattice just raises the next question: How did the lattice get its six-fold symmetry? It is the “Why 6” question all over again.
We’ll address this latter problem first. Why is the lattice hexagonal? A common answer is that the shape of the water molecule forces the molecules to link up into 6-sided rings. Though true, it conflicts with another, little-known fact about water: depending on the water pressure and temperature, water can crystallize into, at last count, 14 other lattices, only two of which are hexagonal. That is, the water molecule’s shape does not always force the lattice into hexagons. But we happen to live under the same conditions that favor ordinary hexagonal ice, also called ice 1h (the ‘h’ standing for hexagonal), and not, for example, cubic ice (ice 1c) or tetragonal ice (ice 9). One could argue that ice 1h is the more natural form, as it requires neither very low temperatures nor any externally applied pressure. So, at least in this ‘natural’ form of ice, the shape of the water molecule produces forces that link the molecules into a lattice of hexagonal rings.
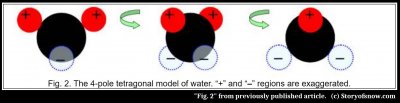
But what are these forces and how do they produce hexagonal rings? Bentley thought the forces were electromagnetic and in 1910 proposed an electromagnetic water model to help explain the six-sided nature of ice. The water molecule in his model(2) had two positive and two negative electrical poles plus some lesser “secondary” poles. I don’t know why he chose these numbers or where the poles were located, but his basic idea was useful. And it was far ahead of its time. In 1933, twenty-three years later, Bernal and Fowler, two pioneering ice physicists, proposed a four-pole model of water to help explain the structure of ice. But their pole model didn’t get much attention until it morphed into the more accurate “tetragonal” four-pole model in 1951. In this model, the two hydrogens are the two positive poles, and the two “lone-pair orbitals” on the other side of the oxygen are the two negative poles, as shown in figure 2. These negative poles, which are predicted by quantum mechanics, are shown as the dotted light-blue spheres. And just as Bentley had included additional secondary poles, later models added poles of weaker charge. Although we’ve known for some time that the bonds in ice are the more complex hydrogen bond, the simpler pole model here is still used to study ice because it is easier to calculate with.
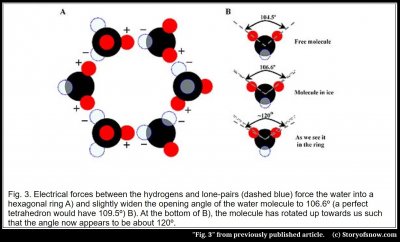
In this model, the positive pole of a molecule attracts to the negative pole of another, forming a bond; similarly, the molecule’s remaining three poles attract three other molecules. As a result, each molecule bonds to two other molecules in the ring, as shown in Fig. 3A, as well as to a neighboring ring and to a ring either above or below.
The hexagon shape occurs because the angle between the two poles on a molecule lies close to that needed for a corner of a hexagon. In particular, this angle for a free molecule (i.e., not bound in ice or liquid) equals 104.5º (see figure 3B), which lies just 5º less than the 109.5º needed to be a corner of a hexagon. This 109.5º is less than the 120º between sides of a flat hexagon because the ring must “crumple” to form bonds to the rings above, below, and beside the ring. So the tetragonal nature of water naturally leads to a hexagonal lattice(3). As to why the water molecule is tetragonal, the answer involves the quantum electrodynamics of oxygen and hydrogen, and best left for those with much more time.
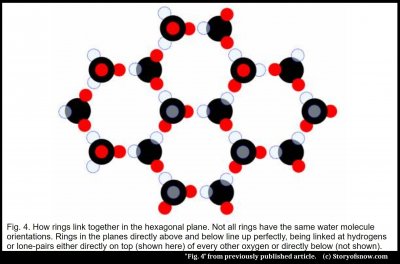
As an aside, the tetragonal bonding leads to some curious and important properties of ice. The resulting hexagonal structure is relatively open, with large empty spaces in the rings, and for this reason ice 1h will float on liquid water. Also, as mentioned above, if we pay attention to the hydrogens, we see that the rings are not really symmetric. Moreover, the hydrogen positions have no order; notice in figure 4 below how each ring is different from its neighbors. And this lack of order leads to the curious electrical properties of ice – properties that include their being the electrical power source of thunderstorms(4).
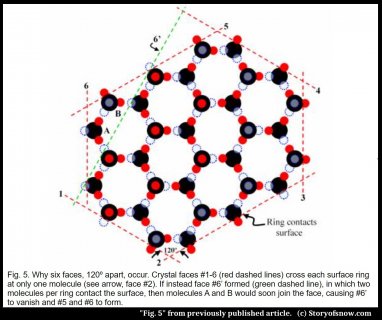
So the water molecule’s shape produces the microscopic hexagons, but how can this affect the surface of a crystal perhaps a million time larger? The answer involves looking at what happens where a ring contacts a crystal surface. Molecules on the surface experience unequal forces – they are pulled more towards the inside of the crystal – but these forces depend on which parts of the rings contact the surface. When only one molecule from each such hexagonal ring lies at the surface, like in the surfaces marked by red dashed lines in Fig. 5 below, the forces make that surface grow relatively slowly. And in the world of growing crystals, the slow-growing faces are the ones that spread out along the crystal, effectively erasing the other faces. It may seem strange, but for crystal faces, the fast-growers essentially burn themselves out and vanish, while the slow-growers dominate. Sometimes it pays to be slow.
Here’s a specific example. In going around the crystal of figure 5, notice that the ring corners stick out at the surface for crystal faces #1–6. With only ring corners on the surface, the crystal can have neither more than six, nor less than six faces(5). Moreover, these faces all intersect at 120º corners. But if the crystal instead had a surface consisting of ring sides instead of ring corners, such as the green-dashed face #6’ instead of the red-dashed #6, then two corners would have angles of 90º and the crystal would have only five sides(6). In this case, the surface forces would be such that new molecules marked A and B would soon attach, effectively replacing face #6’ by faces #5 and 6, leaving the crystal with six sides (not including top and bottom) and six equivalent 120º corners. So this is how the microscopic internal hexagonal rings produce six, and not four, five, or seven sides of the crystal.
Now, for the crystal to actually look the same when rotated by 1/6 of a turn, and be big enough for us to notice, a large, roughly symmetric six-pointed star must form. This requires three other things to happen: First, the crystal must grow thin and broad, meaning that the top and bottom faces must grow much slower than the six side faces. Second, the corners must grow outward faster than the rest of the six faces. And third, each of the six branches should grow at nearly the same rate. As to why the crystal grows so thin, this was one of the first questions Kepler asked about snow. Snow doesn’t always grow so thin; for some still unknown reason this happens only within a narrow temperature range. And how the second and third occur has some interesting aspects and mysteries(7) that will be left for discussion elsewhere. But note that whether or not a crystal is symmetric, adjacent faces differ in angle my multiples of 120º (or 60º if some faces vanish) for the reasons described here.
In 1915, Bentley wrote(8) that he could
“…hardly escape the conviction that the mysterious something that causes the crystals to grow outward only at certain points and to divide into six is electromagnetic in nature,…”.
Indeed, though we’ve made many advances in our knowledge of water, at the bottom, the molecules’ electromagnetic interactions ultimately lead us to the number six, though the symmetry requires quite a bit more.
--JN
References and notes
1) Johannes Kepler, The Six-Cornered Snowflake: A New Year’s Gift. translation from Latin, Paul Dry Books, 2010.
2) Duncan Blanchard, The Snowflake Man, McDonald & Woodward Publishing Co, Blacksburg, Virginia, 1998, pg. 147.
3) This tetragonal nature can also lead to a cubic lattice, with 4-fold symmetry, but it cannot lead to any structure with 5- or 7-fold symmetry; indeed, no crystal can have these symmetries – they are mathematically impossible.
4) See my article in the Feb. 22, 2022 post “The Jericho Farmer and the Electric Crystals”:
https://www.storyofsnow.com/blog1.php/the-jericho-farmer-and-the.
5) Not always true. For example, the branched crystal in figure 6 shows 90 faces (not including top and bottom). But the most important point here is that the resulting angle between faces are always factors of 60º.
6) Actually, depending on the position of face 6’, there could be 5, 6, or 7 faces, and one or two angles could be 150º. But the argument still holds.
7) I analyze these topics in detail in my article “Branch Growth and Sidebranching in Snow Crystals” Crystal Growth & Design, vol. 5, 2005, pp 1509–1525. http://www.storyofsnow.com/media/blogs/a/Snow branching paper.pdf
8) See ref. 2, pg. 153.